
Here, we present an exercise that uses the Titanic datasets and that shows students the general usefulness of mixed methods. We often do the exercise in three hours, but the time obviously varies greatly according to how much time is taken to go into depth in specific steps.
Prerequisites
For these exercises, students need a basic understanding of quantitative and qualitative methods, some knowledge of SPSS and/or R as well as of MAXQDA, and laptops that have either SPSS or R and MAXQDA installed. One of the advantages of R is that it is free. Unfortunately, we cannot yet offer a coded version of the Titanic dataset in a free qual software (like RQDA). You can however start with a free MAXQDA trial.
Ressources
Before going any further, you might find these ressources useful, if not essential, to carry out the exercise.
1. Introduce the exercise
a. Catch their attention: Have students whistle Céline Dion’s “My heart will go on”, or show them a few seconds of the trailer for the Titanic film.
Inform them of important facts:
- the Titanic hit an iceberg on April 14, 1912, at 11:40 p.m. and sunk completely about 2 hours and 40 minutes later.
- 2207 individuals were on board at the time of the collision and only 710 survived, despite the fact that the lifeboats could have saved 1178, so they have been used at only 60% of their capacity.
- The survival rates of individuals differed greatly according sex, classes, types of crew.
b. State the research question: What were the causes / mechanisms that led individuals on the Titanic to survive or perish?
This step is important because we want to show students that mixed methods are not interesting in themselves, but only have legitimacy if they are able to give a more valid answer to a research problem than a mono-method approach.
c. Preliminary theorizing: have students find explanatory variables that may lead to higher or lower probability of surviving on the Titanic. Students come up with variables like class, gender, physical strength, social ties, location of the cabins, etc.
Make
a sketch on the blackboard of these variables. For every independent
variable mentioned, ask students to specify the “causal story” or
“causal mechanism” of how exactly this explanatory variable might have
influenced the response variable.
For example, if they mention
“class”, ask: how did that work exactly? They may say: people in
first-class accommodation had more money than people in the lower-class
cabins, and they may have bribed the crew to allow them onto the
lifeboats. We encourage students to be as precise as possible for every
assumed mechanism.
2. Exploratory quantitative data analysis
Have students do some exploratory quantitative data analysis in SPSS or R with the variables that they have found in the previous step: class, gender, age, and survived/perished…
For example, you can copy/paste the syntax below (Textboxes have numbers related to our article):

Unfold for the syntax in R
###################################
Textbox 3: Exploratory data analysis – R
###################################
library(dplyr)
library(tidyr)
library(ggplot2)
library(forcats)
library(purrr)
# read in data (your own location file)
Titanic_Mixed <- read.csv(“~/Dropbox/2019_neu/02_Projects/P_Titanic/Titanic_Website/DATASET_QUAN/Titanic_Mixed.csv”)
# make it a tibble
data <- tbl_df (Titanic_Mixed)
# recode some variables
data %
mutate (lived = recode(factor(lived), “0” = “perished”, “1” = “survived”)) %>%
mutate (sex = recode(factor(sex),”0″ = “male”, “1” = “female” )) %>%
mutate (testimony = recode(factor(testimony), “0” = “no”, “1” = “yes”)) %>%
mutate (group = recode (factor(group), “0” = “Single”, “1” = “Single w/servant”,
“2” = “Couple”, “3” = “Couple w/kids”, “4” = “Couple w/servant”,
“5” = “Single parent w/kids”, “6” = “Family w/servant”, “7” = “Family/friends”,
“8” = “Crew groups”, “9” = “Family/friends w/kids”))%>%
mutate (country_5cat = recode (factor(country_5cat), “0” = “England”, “1” = “Ireland”, “2” = “Sweden”, “3” = “USA”,
“4” = “Others”))%>%
mutate (country_3cat = recode (factor(country_3cat), “0” = “England”, “1” = “USA”, “2” = “Others”))%>%
mutate (classcrew = recode (factor(classcrew), “1” = “1st class passenger”, “2” = “2nd class passenger”,
“3” = “3rd class passenger”, “4” = “A la carte crew”, “5” = “Deck crew”,
“6” = “Engine crew”, “7” = “Victualling crew”)) %>%
mutate (classcrew1 = recode (factor(classcrew1), “1” = “1st class passenger”, “2” = “2nd class passenger”,
“3” = “3rd class passenger”, “4” = “Crew”)) %>%
mutate (age_cat = recode (factor(age_cat), “1” = “0-14”, “2” = “15-30”,
“3” = “31-40”, “4” = “41-50”, “5” = “51-60”,
“6” = “61+”, “99” = “NA”))%>%
mutate(age = as.numeric(age))%>%
mutate(boatorder = as.numeric(boatorder))%>%
mutate(boatside = recode(factor(boatside), “0” = “Starboard”, “1” = “Port”))
glimpse(data)
# (1) Analysis of bias in testimonies : example gender
options (digits = 3)
all %
group_by(sex) %>%
summarize (All = n()) %>%
mutate (percent = All/sum(All) * 100)%>%
select (- sex)
survivors %
filter(lived == “survived”) %>%
group_by(sex) %>%
summarize (Survivors = n()) %>%
mutate (percent = Survivors/sum(Survivors)* 100)%>%
select (- sex)
testifiers %
filter(lived == “survived” & testimony == “yes”) %>%
group_by(sex) %>%
summarize (Testifiers = n()) %>%
mutate (percent = Testifiers/sum(Testifiers)*100)
bias_table <- cbind(testifiers, survivors, all)
bias_table
#(2) Frequencies response variable
data %>%
group_by(lived)%>%
count()%>%
ungroup()%>%
mutate(percent = n/sum(n))
# (3) Frequencies explanatory variable
crosstabs <- function(df, Var1, Var2 ){
df %>%
group_by(!! Var1, !! Var2) %>%
summarize (n = n()) %>%
mutate (perc = n/sum(n)* 100) %>%
print()
}
explanatory_vars <- list(“sex”, “classcrew”, “age_cat”, “boatnumber”,
“boatside”, “child”, “country_5cat”, “testimony”)
explanatory_vars1 <- list(“sex”)
for (i in 1: length(explanatory_vars)){
crosstabs(data, quo(lived), quo(eval(parse(text=paste0(explanatory_vars[[i]])))))
}
glimpse(data)
# (4) Barchart
data %>%
group_by(sex)%>%
summarize (survival_rate = mean(lived == “survived”))%>%
ggplot(aes(x = sex, y =survival_rate))+
geom_bar(stat = “identity”, fill = “darkblue”)+
labs(x = “”, y = “Percentage survived”, title = “Survival rate on the Titanic according to Gender”)
data$sex <- relevel(data$sex, ref = “female”)
data %>%
group_by(classcrew, sex,lived) %>%
summarise(n = n()) %>%
mutate (perc = n/sum(n)* 100) %>%
filter (lived == “survived”) %>%
ggplot(aes(classcrew, perc, fill = sex))+
geom_bar(stat = “identity”, position = position_dodge(preserve = “single”))+
labs(x = “Class & type of crew”, y = “Percent”,
title = “Survival ratio according to class/crew & Sex”)+
theme(legend.title = element_blank())+
scale_fill_manual(values=c(“firebrick”, “dodgerblue3”))+
geom_text(aes(label = scales::percent(perc/100), y = perc + 2.2),
position = position_dodge(width = 1), size = 3)

Unfold for the syntax in SPSS
***********************************
Textbox 2: Exploratory quantitative analysis – SPSS
***********************************
*** (1) Analysis of bias in testimonies: example gender
crosstabs testimony by sex by lived
/cells count row
/statistics.
*** (2) Frequencies response variable
Frequencies lived /bar chart.
*** (3) Frequencies explanatory variables
Frequencies sex classcrew age_cat boatnumber boatside child country_5cat testimony / barchart.
Graph
/histogram age.
*** (4) Some simple crosstabs
crosstabs lived by classcrew sex
/cells count col
/statistics.
crosstabs lived by classcrew by sex
/cells count col
/statistics.
Graph
/bar(grouped)=mean(lived) by classcrew by sex.

Have students summarize what they have learned from this exploratory analysis. They/we normally come to the following intermediate conclusions:
(1) Analysis of bias in testimonies: example gender. There is an important bias in our sampling of those providing a testimony – because it was only those that survived that gave a testimony! This is “selecting on the dependent variable”, with all its known problems. However, there are even more instances of bias, because men and women did not survive with equal probability. The gender ratio of all individuals on the Titanic was 78% men to 22% women; of survivors, it was 50.1% men to 49.9% women; of those testifying, 57.5% men to 42.5% women. This means that we have a double selection process: women are much more likely to be in the survivor category, but, of the survivors, men are more likely to be in the testifier category. We urge students to keep this very bias in mind when interpreting our insights from the qualitative sample.
(2) Response variable. Of 2207 individuals in our dataset, 1497 (67.8%) perished, and only 710 (32.2%) survived.
(3) Frequencies explanatory variables. We look at the different frequency tables. We note, for example, that there were many more men (78%) on the Titanic than women (22%), and many more third-class (32.1%) than first-class (14.7%) and second-class (12.9%) passengers. Roughly 40% of the individuals on the Titanic were crew members.
(4) Some simple crosstabs. We look at survival by gender, class/crew, and gender*class/crew.
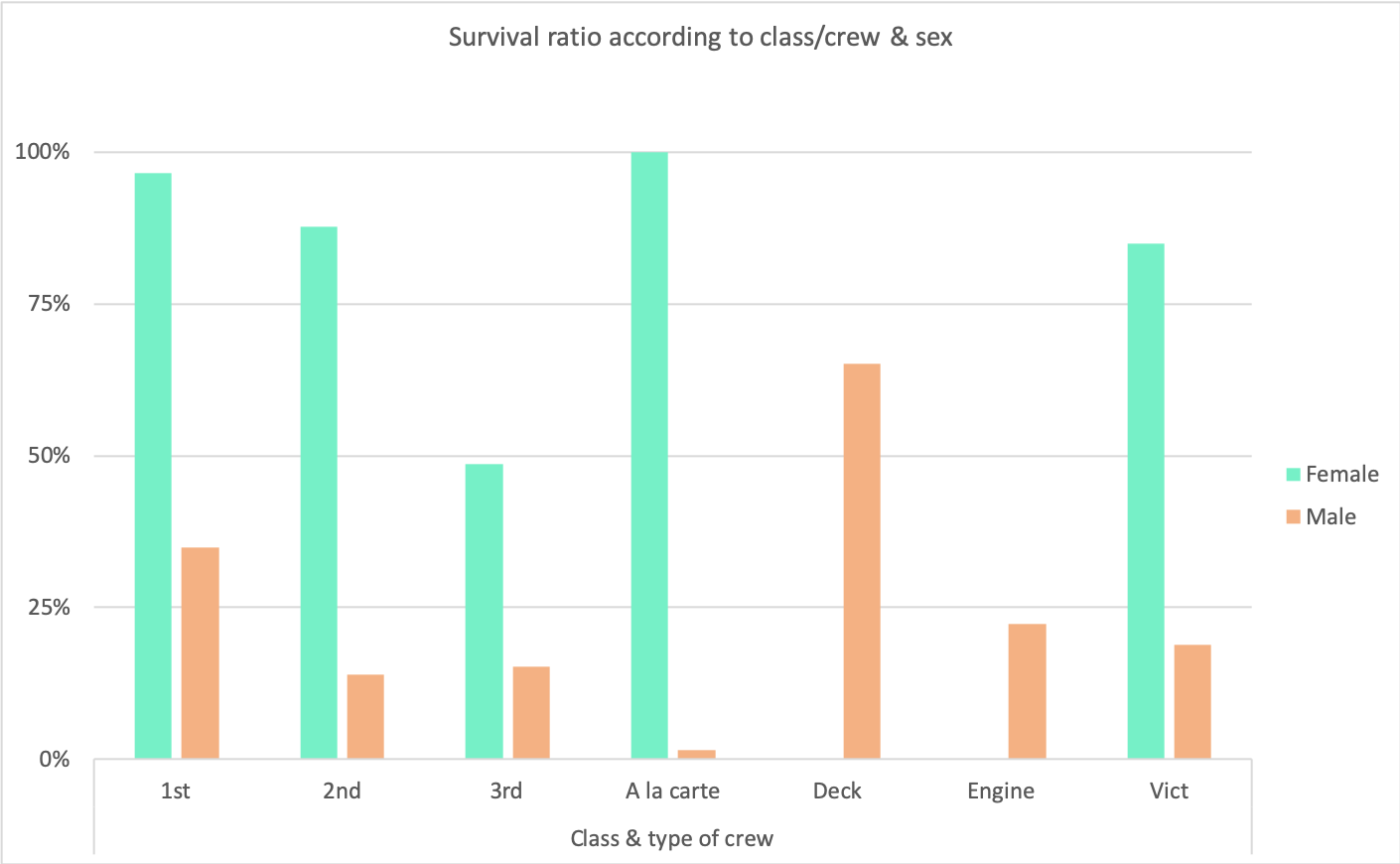
As described in Stolz, Lindemann and Antonietti (2019: 1627), we find that (see also Figure 1):
- Women across all classes and types of crew generally have a higher likelihood of survival than men (e.g. first-class female passengers, 96.5% vs. first-class male passengers, 34.4%), the one exception being that male deck crew have a higher likelihood of survival than third-class female passengers.
- Higher-class passengers generally survive more often than lower-class passengers (e.g. first-class female passengers, 96.5% vs. second-class female passengers, 84.9%, vs. third-class female passengers, 48.6%), the one exception being that there is no significant difference between second-class and third-class male passengers.
- We find interactions between gender and class. There is a significant difference between first-class and second-class female passengers who survive (more than 80%) and third-class female passengers who survive (only 48.6%); for men, the major difference is between first-class male passengers who survive (34.4%) and second-class and third-class male passengers, who have very similar survival rates of 14% and 15% respectively. The men belonging to the restaurant crew (A la carte) have the lowest survival rate of all groups of men, with only 1.5% (both women belonging to the restaurant crew survive). Male deck crew have the highest likelihood of survival of all groups of men (63.6%).
3. Exploratory qualitative data analysis
Have students do some exploratory qualitative analysis with MAXQDA. We introduce this part by telling students two things:
(1) They cannot possibly provide a qualitative analysis of this material in the short time available in the exercise. Good qualitative analysis means becoming thoroughly acquainted with the material as a whole, reading through all the testimonies, and carefully coding, comparing, and recoding them, etc. Here, the goal is to look at some selected testimonies and coded material to understand the way that mixed methods analysis can be put into practice.
(2) This analysis is not about how to code, since the coding is already provided. Also note that we not only coded the content of the testimonies, but also created document variables for each testimony such as “gender”, “age” or “boat” of the testifier. For a description of how the coding was done, see Stolz & Lindemann (2019).
We recommand different steps to follow in MAXQDA to carry out the analysis (again, Textboxes have numbers related to our article).

Unfold for the step-by-step procedure in MAXQDA
(1) Compare first-class and third-class women
In MAXQDA, in the window with the list of codes, select the “Exercise” code. Right-click on it. A menu pops up. Select “Activate”.
Now go to tab mixed methods. Click activation by document variables. Activate first-class women, by putting [Gender] = F AND [Class] = 1 into the right-hand box. Click “Activate”. In the “View” menu, select “Selected Codings”. You should now see parts of the testimonies of three first-class women. Read through these testimonies.
Now change to see three third-class women. Click activation by document variables. Activate third-class women, by putting [Gender] = F AND [Class] = 3 into the right-hand box. Click OK.You should now see parts of the testimonies of three third-class women. Read through these testimonies. What is different in the accounts provided by first- and third-class women?
(2) Compare first-class and third-class women: codings about filling rule “women and children first”
Select the Exercise code. Right-click on the “Exercise” code. Select “Deactivate”. In the code “Filling rules” (experiencd), select the subcode “Women & Children first”. Right-click on it. Select “Activate”. Now go to mixed methods tab. Select all first-class women as before. In the view menu, select “Selected Codings”.
You should now see all coded testimonies where surviving first-class women say that the filling rule “women and children first” was used for their lifeboat. Do the same thing for third-class women, and compare.
(3) Make crosstabulation Authority acceptance * Boatorder
In MAXQDA, in the document window, activate all the documents (Boat 1 to Collapsible A).
In the code window, activate all codes under “Authority acceptance”.
Go to tab “Mixed Methods”. Go to Crosstabulation. Click on the Variable “Boat” in the left-hand window. Click below on “Insert all values into the table”. Click on the arrow. This puts all boats into the right-hand window.
Now change the order of the boat (manually change the “Values” for each one and remove “boat 99”) until you have the following order (order in which lifeboats left the Titanic):
[Boat] = 7
[Boat] = 5
[Boat] = 3
[Boat] = 8
[Boat] = 1
[Boat] = 6
[Boat] = 16
[Boat] = 14
[Boat] = 12
[Boat] = 9
[Boat] = 11
[Boat] = 13
[Boat] = 15
[Boat] = 2
[Boat] = 10
[Boat] = 4
[Boat] = C
[Boat] = D
[Boat] = B
[Boat] = A
Click on OK. What generalizations can be made about authority acceptance during the filling of the lifeboats?
(4) Make crosstabulation Filling rules * Boatorder
In MAXQDA, in the document window, activate all the documents (Boat 1 to Collapsible A). These documents should now appear in red.
In the code window, activate all codes under Filling rules/Experienced. These codes should now appear in red.
Go to tab “Mixed Methods”. Go to Crosstabulation. Click on the Variable “Boat” in the left-hand window. Click below on “Insert all values into the table”. Click on the arrow. This puts all boats into the right-hand window.
Now change the order of the boat (manually change the “Values” for each one and remove “boat 99”) until you have the following order (order in which lifeboats left the Titanic):
[Boat] = 7
[Boat] = 5
[Boat] = 3
[Boat] = 8
[Boat] = 1
[Boat] = 6
[Boat] = 16
[Boat] = 14
[Boat] = 12
[Boat] = 9
[Boat] = 11
[Boat] = 13
[Boat] = 15
[Boat] = 2
[Boat] = 10
[Boat] = 4
[Boat] = C
[Boat] = D
[Boat] = B
[Boat] = A
Click on OK. Did the application of filling rules change during the process of filling?
(5) Make crosstabulation Filling rules * Boatside
In MAXQDA, in the document window, activate all the documents (Boat 1 to Collapsible A). These documents should now appear in red.
In the code window, activate all codes under Filling rules/Experienced. These codes should now appear in red.
Go to tab “Mixed Methods”. Go to Crosstabulation. Click on the Variable “Boatside” in the left-hand window. Click below on “Insert all values into the table”. Click on the arrow. This puts all levels of “boatside” into the right-hand window. Now remove [Boatside] = 99
Click on OK. Use row percentages. Did the application of filling rules differ on port and starboard?
(6) Make crosstabulation Way to the boat deck * Classcrew
In MAXQDA, in the document window, activate all the documents (Boat 1 to Collapsible A), except “Other witnesses”. These documents should now appear in red.
In the code window, activate all codes under “Arrival time on deck” and “Way to boat deck – Experienced”. These codes should now appear in red.
Go to tab “Mixed Methods”. Go to Crosstabulation. Click on “Class” in the left-hand window. Click below on “Insert all values into the table”. Click on the arrow. This puts all classes into the right-hand window. Now change the order of the classes until you have the following order:
[Class] = 1
[Class] = 2
[Class] = 3
[Class] = Deck crew
[Class] = Restaurant crew
[Class] = Engine crew
[Class] = Victualling crew
Click on OK. Did different classes differ in terms of their experience when trying to get to the boat deck?
The plan that we provide in their handout can be useful to understand how the filling of the board varied between port and starboard. We take the advantage to put it here for you too!

Have students summarize what they have learned from this exploratory qualitative analysis. They/we normally come to the following intermediate conclusions:
(1)/(2) Compare first-class and third-class women: Time is important. It seems that first-class passengers arrived on the boat deck (where the lifeboats were) earlier than second-class passengers, who in turn arrived earlier than third-class passengers. We point out to students that we could test this idea with our quantitative dataset in a next step. We also encourage students to dig further into the data to find the exact reasons for why this was the case.
(3) Crosstabulation Authority acceptance * Boatorder: The crew was important when filling the boats. This is a very important point because it means that the rational behaviour of individuals is of very limited use when explaining survival probabilities on the Titanic. The crew was very much in control of what happened, and the final outcome depended largely on how they put their rescuing and filling rules into practice.
(4) Crosstabulation Filling rules * Boatorder: The rule “Women and children first” was used in all boats, except the two last ones. The rule “If no more women – fill up with men” was used in only some boats and not others. The rule “Couples first” is only mentioned for the two first boats. The rule “Fill with anybody” is mentioned only for the two first and the two last boats. We explain to students that, with more time, one would now go deeper into the material to understand the reason for these differences. Clearly, at the beginning of the filling process, the practice was not yet clearly defined. At the end of the process, the water was already very high and an orderly filling was not possible anymore.
(5) Crosstabulation Filling rules * Boatside: Filling rules were different on port and starboard. Clearly, the rule “Women and children first” was interpreted differently on Port and Starboard. On Port, it was understood as “Women and children only”. On Starboard it was interpreted as: “Fill up with women and children – but if there are no more women and children around, fill up with men”. We explain that, once we had noticed this, we had the idea of creating the variable “boatside” for our quantitative dataset to test this hypothesis.
(6) Crosstabulation Way to the boat deck * Classcrew : The way to the boat deck was different for different classes. For example, lower-class passengers had a much longer and more difficult way to the boat deck.
We explain to students that what we have effectively done in our qualitative analysis is to show the meaning and function of the quantitative variables in the context of the “social game” that was played on the Titanic. This social game used rules, representations, objects, actions and interactions that students had not thought of when making their initial hypotheses. The reason is that they were not familiar enough with the specifics of the “social game”. Their “everyday assumptions” about the Titanic were incorrect (for example that first class passengers were wealthier and bribed the crew to enter the boats). This might happen for any mono-quantitativeresearch in which the researcher is not familiar enough with the case in hand.
4. Revisit the quantitative data
Once students have a better understanding of the social game played on the Titanic, and new ideas about what might be important in explaining survival probabilities, we invite them to do a second round of quantitative analysis. This round incorporates analyses that look at the specific time that individuals boarded a lifeboat and the side of the Titanic from where they boarded the lifeboat.
For example, you can copy/paste the syntax below (again, textboxes have numbers related to our article). Note for SPSS: The “boatentertime” variable indicates 40.00 for 00:40 a.m. and 120.00 for 1:20 a.m.

Unfold for the syntax in R
########################################
Textbox 6: Further quantitative analysis in R
########################################
data$boatside <- relevel(data$boatside, ref = “Port”)
data %>%
filter (boatside != 99)%>%
group_by(sex, classcrew, boatside) %>%
summarize (n = n()) %>%
mutate(percent = n/sum(n)* 100)
data %>%
filter (boatside != 99)%>%
group_by(sex, classcrew, boatside) %>%
summarize (n = n()) %>%
mutate(percent = n/sum(n)* 100)%>%
ggplot(aes(classcrew, percent, group = sex, fill = sex))+
geom_col(position = position_dodge(preserve = “single”))+
facet_wrap(~ boatside )
# (1) Calculate filling over time according to class / crew
data %>%
filter (boatorder != 99)%>%
group_by(sex, classcrew, boatorder) %>%
summarize (n = n()) %>%
mutate(percent = n/sum(n)* 100)
# (1bis) Plot lifeboat filling over time according to class / crew (Figure 1)
data %>%
filter (boatorder != 99)%>%
filter (boatside != 99)%>%
group_by(boatside, classcrew1, boatorder) %>%
summarize (n = n()) %>%
mutate(percent = n/sum(n)* 100)%>%
ggplot(aes(boatorder, percent, group = classcrew1, fill = classcrew1))+
geom_col(position = position_dodge(preserve = “single”), width = 1.5)+
facet_wrap(~ boatside )+
labs(title = “Lifeboat filling over time according to class/crew and Port/Starboard”, x = “Minutes after impact”, y = “Percent”)+
theme(legend.title = element_blank())
# (2) Plot lifeboat filling according to gender and Port/Starboard (Figure 3)
data %>%
select(boatside, sex1, boatentertime) %>%
filter(boatside != “99”) %>%
filter(boatentertime %
group_by (boatside, sex1, boatentertime) %>%
summarize (n = n()) %>%
mutate(cum_n = cumsum(n)) %>%
ggplot(aes(x = boatentertime, y = cum_n, group = sex1, color = sex1))+
geom_line()+
facet_wrap(~ boatside)+
labs(title = “Lifeboat filling according to gender and Port/Starboard”, x = “Minutes after impact”, y = “Entered lifeboat”)+
scale_colour_discrete(labels = c(“male”, “female”))+
theme(legend.title = element_blank())

Unfold for the syntax in SPSS
*******************************************
Textbox 5: Further quantitative analysis in SPSS
*******************************************
USE ALL.
COMPUTE filter_$=(boatentertime < 130).
VARIABLE LABELS filter_$ ‘boatentertime < 130 (FILTER)’.
VALUE LABELS filter_$ 0 ‘Not Selected’ 1 ‘Selected’.
FORMATS filter_$ (f1.0).
FILTER BY filter_$.
EXECUTE.
*** (1) Crosstabs: class and boarding time
crosstabs boatentertime by classcrew
/cells count row
/statistics
/barchart.
*** (2) Crosstabs : class, sex and boarding time
crosstabs boatentertime by sex by boatside
/cells count col
/statistics.

Have students summarize what they have learned from their further quantitative analysis. In short, students test the new ideas that they had during their qualitative analysis. We bring together the results in class:
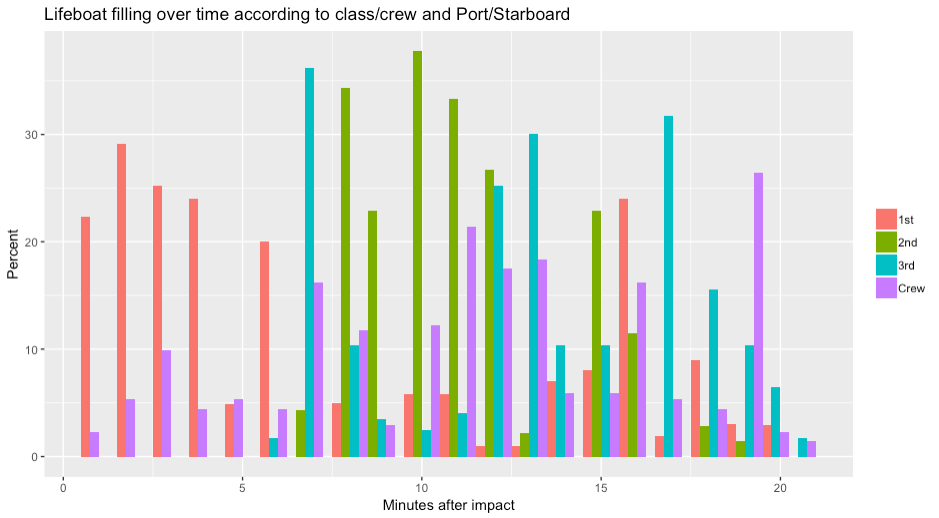
(1) Class and boarding time : As suspected, higher-class passengers had a higher chance of boarding the lifeboats that left the Titanic earlier. While the qualitative material allowed us to create the hypothesis, analysis of the quantitative data leaves no doubt that this was in fact the case. They should have created the same figure as below (only possible in R).
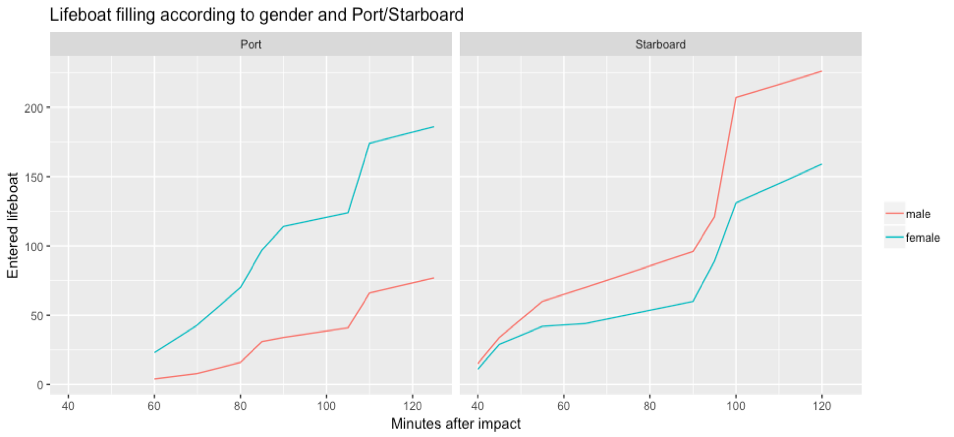
(2) Class, sex and boat side: The quantitative data confirm that rules of filling were applied differently on port and starboard. In fact, on starboard, more men boarded lifeboats than women. They should have come up with the same figure as below (only possible in R). This was the case in spite of the fact that the rule “women and children first” was in fact applied, and can be explained by the fact that the rule “when there are no more women, fill with men” was applied on starboard (but not on port).
5. Wrapping up
In a final part, we wrap up the exercise with the students and highlight a few general points. We often do this by asking students the following questions, discussing their responses, and then making the following points (if they have not already been made by the students themselves).
(1) Have we learned more by using both qualitativeand quantitative data than we would have had we only used one method? Are our conclusions more valid than if we had had only quantitative or only qualitative data?
Students overwhelmingly answer in the affirmative. We then ask: why exactly? The group comes up with something like the following: with the help of the qualitative dataset, we were able to unearth information about the “social game” that we did not initially have to interpret quan-information: this information concerned the importance of the crew, the importance of rules, and the importance of time. We were able to understand the meaning and function of the quantitative variables in the context of the social game better. If students challenge this point, we remind them of their initial hypotheses that almost invariably did not include a large number of the finer points found by qualitative analysis. Conversely, we were able to quantify, correlate, and generalize many insights gleaned from the qualitative material that would have remained less convincing without quantification (frequency distributions; correlations/bivariate distributions; size and significance of effects). The conclusions we drew are called meta-inferences, which can be defined as conclusions concerning the phenomenon to be analyzed based on the analysis of qualitative and quantitative data.
(2) Why do the datasets allow us to make meta-inferences so well?
In the discussion, we come up with something like the following: a first point is that the data stem from the same case and the same people. This is an important point. Imagine that we had had quantitative data from the Titanic, but qualitative interviews with passengers of a different ship that had also sunk (say, the Costa Concordia in Italy). It would have been very difficult to obtain useful meta-inferences. A second point is that we coded the qualitative material in such a way that it allowed us to provide a systematic description of the mechanisms leading to the outcome of interest. Imagine that we had coded for “dress code” or “metaphors”. This might have been interesting – but it would not have helped us with our research question and would not have allowed us to make useful meta-inferences.
(3) What are the limits to our analysis?
We discuss the limits to our analysis with students. We have already mentioned this when we discussed our data, and we do not need to repeat it in detail here. Suffice to say that we talk about (a) the “survivorship-bias”: clearly, only survivors can tell their story, and much of what happened to those who perished will remain unknown forever; (b) the fact that our view of the filling of the lifeboats is more reliable than our view of the way to the boat deck, since we can cross-check so many accounts with the former, but not with the latter.
(4) How can we summarize the overall findings?
(This summary contains some findings that were not seen in the exercise.)
We ask students to give a short summary of the overall results. We then give our own version that goes something like this (Stolz, Lindemann and Antonietti 2018)[i]: Women and children survived more often than men because of the rule “Women and children first”, which was the one conscious rule that officers and crew applied throughout the process. Whenever women or children were in sight, they were first allowed onto the lifeboats. However, the rule was interpreted differently on starboard (where the boats were “filled with men”, once there were no more women or children in sight) and port (where only women and children, and the members of crew needed to accompany them, were allowed to board). Higher-class female passengers survived more often than lower-class female passengers, because the former arrived earlier on the boat deck, with first-class women passengers arriving earlier than second-class, and second-class earlier than third-class.
Male passengers were able to survive for reasons that changed over time. In the first phase, first-class male passengers were able to survive because of the reluctance of many women to board a lifeboat, and because they were the only men on the boat deck to “fill” the lifeboats.
In the second phase, a number of lifeboats on port were lowered with a very strict rule of “women and children only”, which meant that men (with the exception of male deck crew) only had a very small chance of boarding a lifeboat. The tragedy of second-class male passengers was that they would have been present on the boat deck and in a prime position to “fill” these boats (since many crew members and third-class male passengers had not yet reached the boat deck) – but they were not allowed to do so.
In the third phase, the seriousness of the situation had became obvious, and crew members and third-class male passengers seem to have been more enterprising when “filling” and “surreptitiously boarding” the lifeboats, thereby crowding out both first-class and second-class male passengers. Once in the water, younger men had an edge over older men in surviving until a lifeboat could pick them up (this was rare, however: only one woman survived in this way).
The discrimination against lower classes was not a conscious policy when filling the boats. Rather, it was a combination of several mechanisms: for example, the fact that the cabins of lower-class passengers were much farther away from the boat deck, that access to the boat deck was normally denied to third-class passengers, and that there were fewer stewards to attend to them.




